Preconcetti: vettori e scalari.
Operazioni di moltiplicazione con i vettori sono di 3 tipi e, per la tua gioia, ogni tipo ha le sue regole.
Moltiplicazione di un vettore per uno scalare: il modulo del vettore risultante è pari al prodotto del modulo iniziale per lo scalare (numero), mentre direzione e verso non variano se il numero è positivo, mentre cambia anche il verso se il numero è negativo. $$ \vec{b} = 3\cdot\vec{a} \implies | \vec{b}|=3\cdot |\vec{a}|$$
Prodotto scalare tra vettori: qui c’è bisogno di un po’ di matematica in più. Per ora affidiamoci alla calcolatrice o simili e diciamo che il prodotto scalare tra due vettori restituisce sempre un numero che si ottiene così: $$\vec{a} \cdot \vec{b} = | \vec{a}|| \vec{b}|cos(\alpha)$$
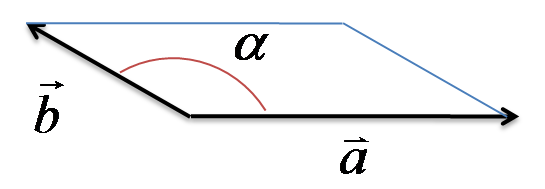
Prodotto vettoriale tra vettori: come sopra sfruttiamo la calcolatrice. Il prodotto vettoriale tra due vettori è sempre un vettore, con modulo pari a: $$\vec{a} \times \vec{b} = | \vec{a}|| \vec{b}|sen(\alpha)$$
mentre direzione e verso si trovano utilizzando la mano destra:
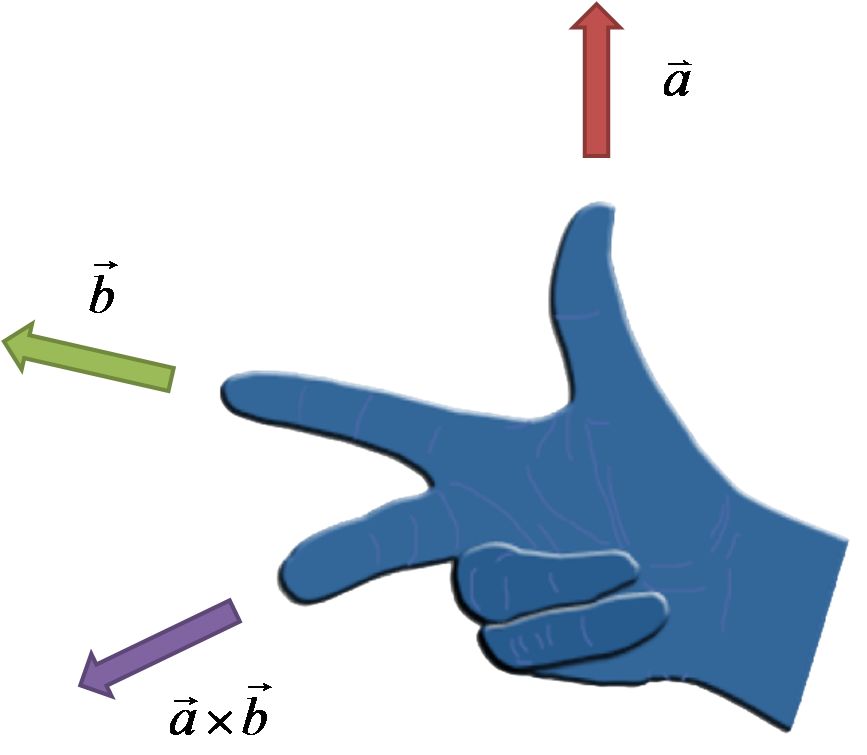
Di fatto, il modulo del prodotto vettoriale è pari all’area del parallelogramma formato tra i due vettori iniziali.