Preconcetti: moto accelerato.
Alla fisica, si sa, piace semplificare la realtà.
Concentriamoci per ora sull’analisi di un moto la cui accelerazione è costante. Un buon punto di partenza è sempre l’esperimento: prendi la Ferrari che hai in garage e prova ad accelerare da 0 a 100 km/h nel minor tempo possibile. Fatto? Bene. Ti sarai accorto, oltre alla difficoltà nel reperire una Ferrari, che sei partito da fermo e dopo un certo tempo hai raggiunto una velocità di 100 km/h. Se si calcola l’accelerazione media per qualsiasi intervallo di tempo e si ottiene sempre lo stesso risultato, significa che l’accelerazione è stata costante. Si parla quindi di moto rettilineo uniformemente accelerato (MRUA per gli amici).
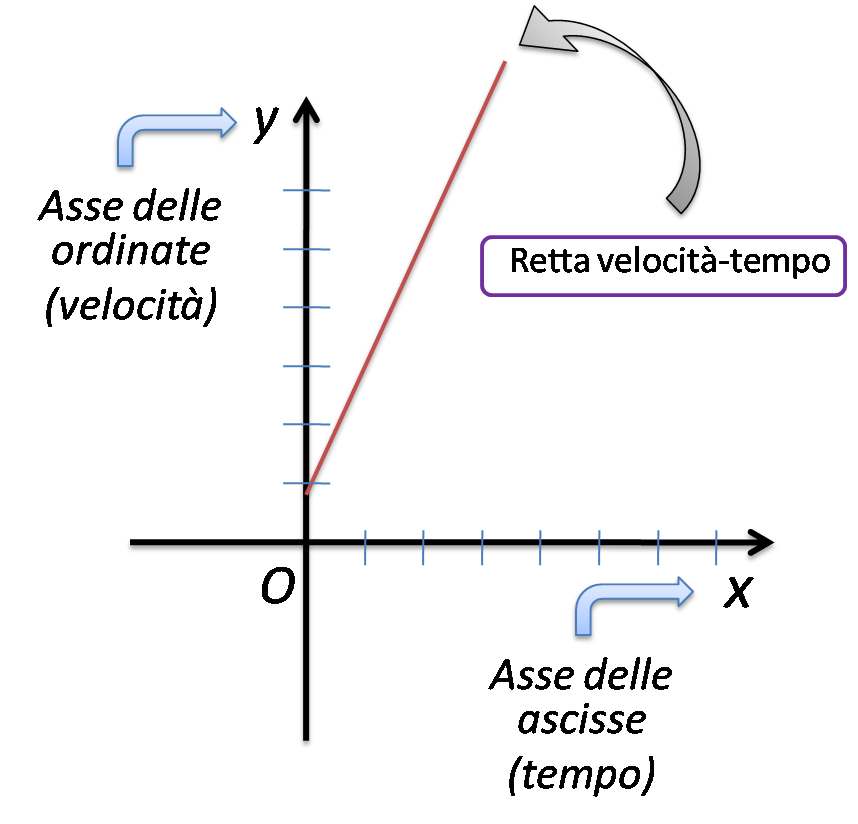
Come vedete è bastato riciclare il grafico usato in precedenza cambiando solamente la grandezza usata per l’asse delle ordinate. La velocità calcolata ad un qualsiasi istante è pari a:
$$v(t) = v_{0} + a \cdot \Delta t$$
dove $\Delta t = t – t_{0} = t$ se $t_{0}=0$, cioè se facciamo partire il cronometro quando inizia il moto.
E se volessi calcolare lo spazio percorso in un certo tempo? Facilissimo, basta ricordarsi che nel caso del moto rettilineo uniforme lo spazio percorso era dato dall’area individuata dalla curva del grafico velocità-tempo. Qui si ragiona allo stesso modo:
Nel caso MRUA, lo spazio percorso è dato dall’area del trapezio individuato dalla curva. La legge oraria è quindi:
$$ \Delta s(t) = \frac{v_{0}+v}{2} \cdot t $$
ma $v = v_{0} + a \cdot t$ e sostituendo:
$$ \Delta s(t) = v_{0} t + \frac{1}{2} a t^{2}$$
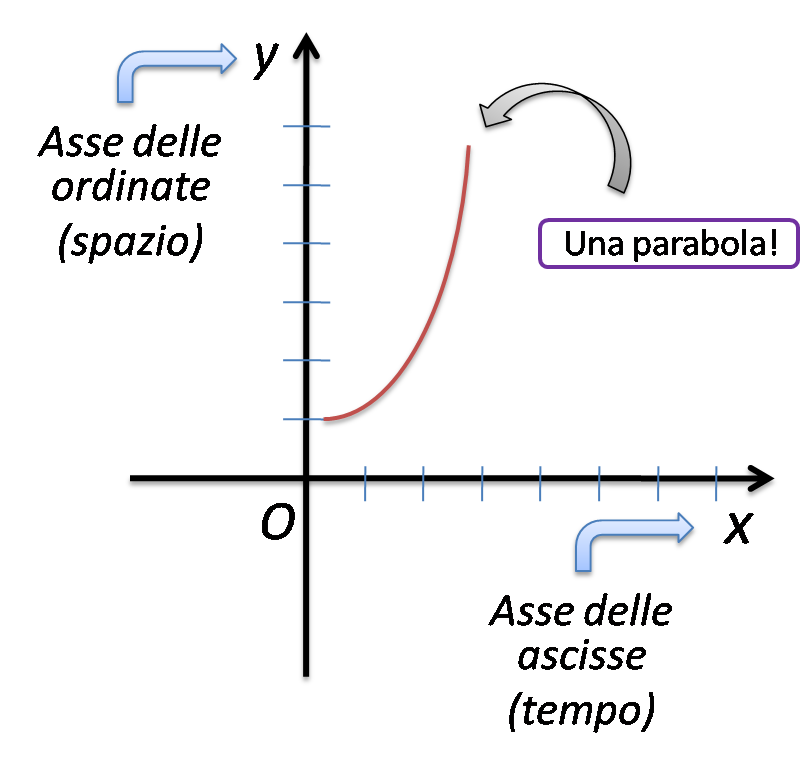
Riportando il tutto nel piano cartesiano si ottiene una parabola (o una sua parte):